hiperbolne funkcije, funkcije koje se geometrijski mogu definirati preko jedne grane jedinične hiperbole y² – x² = 1 analogno kako se trigonometrijske funkcije definiraju preko jedinične kružnice. Obuhvaćaju funkcije: hiperbolni sinus (znak sinh x), hiperbolni kosinus (znak cosh x), hiperbolni sekans (znak sech x), hiperbolni kosekans (znak csch x), hiperbolni tangens (znak tanh x) i hiperbolni kotangens (znak coth x) a također i njima inverzne (area) hiperbolne funkcije: inverzni hiperbolni sinus (znak arsinh x), inverzni hiperbolni kosinus (znak arcosh x), inverzni hiperbolni sekans (znak arsech x), inverzni hiperbolni kosekans (znak arcsch x), inverzni hiperbolni tangens (znak artanh x) i inverzni hiperbolni kotangens (znak arcoth x). Najpoznatija krivulja hiperbolnih funkcija je lančanica, krivulja funkcije hiperbolni kosinus. Hiperbolne funkcije otkrio je 1790. Johann Heinrich Lambert.
Definicijske formule hiperbolnih funkcija:
sinh x = 1/2 (ex – e–x),
cosh x = 1/2 (ex + e–x),
tanh x = (sinh x) / (cosh x),
coth x = (cosh x) / (sinh x),
sech x = 1 / (cosh x),
csch x = 1 / (sinh x).
Veza između hiperbolnih i trigonometrijskih funkcija:
sinh x = –i sin (ix),
cosh x = cos (ix),
tanh x = –i tan (ix),
coth x = i cot (ix),
sech x = sec (ix),
csch x = i csc (ix).
Inverzne hiperbolne funkcije mogu se izraziti s pomoću logaritama:
arsinh x = log (x + √ x² + 1 ),
arcosh x = log (x + √ x² – 1 ),
artanh x = 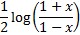 ,
,
arcoth x = 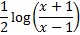 ,
,
arcsch x = 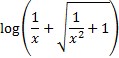 ,
,
arsech x = 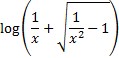 .
.