integral (prema kasnolat. integralis: sastavni, cjelovit, od klas. lat. integer: netaknut, čitav) (znak ∫), funkcija ili veličina koja je ili rješenje diferencijalne jednadžbe ili limes zbroja vrijednosti neke funkcije. Znak integrala potječe od Gottfrieda Wilhelma Leibniza i predstavlja izduženo slovo S (početno slovo od suma, zbroj). U integralnom računu naziv integral uključuje dva bitno različita pojma, određeni integral (limes zbroja infinitezimalno malih dijelova ploštine koji daje ukupnu ploštinu ispod krivulje zadane funkcije, u rasponu između donje i gornje granice) i neodređeni integral (integral kojemu rješenje nije jednoznačno, nego mu se može pribrojiti konstanta bilo koje vrijednosti).
Osnovna pravila integriranja
Zbrajanje i oduzimanje integrala: ∫(f(x) ± g(x))dx = ∫f(x)dx ± ∫g(x)dx.
Množenje integrala konstantom: ∫cf(x)dx = c∫f(x)dx.
Parcijalna integracija (integracija produkta dviju funkcija):
∫f'(x)g(x)dx = f(x)g(x) − ∫ f(x)g'(x)dx.
Određeni integrali
Jednostruki integral je određeni integral jedne varijable po jednodimenzijskome području integriranja. Newton-Leibnizova formula izražava tvrdnju da je jednostruki integral funkcije na zatvorenome intervalu jednak razlici vrijednosti njezine primitivne funkcije u krajnjim točkama intervala:
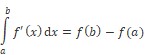 ,
,
gdje je f' neprekidna funkcija definirana i integrabilna na zatvorenom intervalu [a, b] skupa realnih brojeva i f neprekidna funkcija koja je primitivna funkcija funkcije f' na otvorenome intervalu x ∈ (a, b).
Dvostruki integral je određeni integral dviju varijabla po dvodimenzijskome području integriranja. Određuje se uzastopnim računanjem dva jednostruka integrala s pomoću Newton-Leibnizove formule. Može se primijeniti za određivanje ploštine i volumena tijela omeđenoga zadanim plohama. Rezultat ne ovisi o redoslijedu integriranja. Primjerice, ako je područje integracije D zadano dvama neprekidnim funkcijama D = {(x, y) : a ≤ x ≤ b, g (x) ≤ y ≤ h (x)}, tada je dvostruki integral:
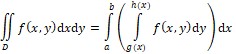 ,
,
Trostruki integral je određeni integral triju varijabla po trodimenzijskome području integriranja a može se primijeniti za određivanje volumena tijela omeđenoga zadanim plohama. Rezultat ne ovisi o redoslijedu integriranja. Ako je područje integracije D zadano trima neprekidnim funkcijama D = {(x, y, z) : a ≤ x ≤ b, h1 (x) ≤ y ≤ h2 (x), g1 (x, y) ≤ z ≤ g2 (x, y)}, tada je trostruki integral:
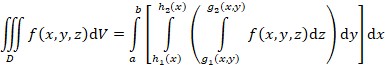 ,
,
gdje je dV = dxdydz element volumena.
Tablica osnovnih neodređenih integrala
∫dx = x + C
∫xn dx = (xn+1 / (n + 1)) + C (za n ≠ –1)
∫dx / x = ln |x| + C
∫ex dx = ex + C
∫ax dx = (ax / ln a) + C (za a > 0, a ≠ 1)
∫cos x dx = sin x + C
∫sin x dx = – cos x + C
∫dx / cos²x = tan x + C
∫dx / sin²x = – cot x + C
∫cosh x dx = sinh x + C
∫sinh x dx = cosh x + C
∫dx / cosh²x = tanh x + C
∫dx / sinh²x = – coth x + C
∫dx / √ a² – x² = arcsin (x / a) + C (za a > 0)
∫dx / (a² + x²) = (1 / a) arctan (x / a) + C (za a > 0)
∫dx / √ a² + x² = ln (x + √ a² + x² ) + C (za a > 0)