potenciranje

potenciranje (prema potencija), unarna osnovna matematička operacija koja broju, varijabli, polinomu, matrici ili nekom drugom matematičkom objektu pridružuje njegovu potenciju, inverzna je korjenovanju. Primjerice, ako je a realni broj, a n prirodni, n-ta potencija od a, simbolički označena s aⁿ, definirana je s aⁿ = a · a · … · a, tj. kao n-struki produkt broja a samim sobom. Kaže se da je a baza, a n eksponent te potencije. Specijalno se a² naziva kvadrat, a a³ kub od a. Za a ≠ 0 pojam se potencije proširuje na sve cijele eksponente definicijom a⁰ = 1, a^–n = 1/aⁿ. Za a > 0 moguće je i daljnje poopćenje na sve racionalne eksponente prema definiciji a^m/n = ⁿ√ a^m . Pojam potencije a^r za bilo koji realni eksponent r definira se kao , gdje je r_k (za k = 1, 2, …) bilo koji niz racionalnih brojeva koji konvergira prema r, tj. 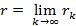. Pokazuje se da takav limes uvijek postoji i neovisan je o izboru niza r_k koji konvergira prema r. Za potencije s proizvoljnim eksponentom vrijede ova pravila: a^r · a^s = a^r+s, a^r/a^s = a^r–s, (a^r)^s = a^rs.