vektorski umnožak

vektorski umnožak (vektorski produkt), vektor kojemu je iznos jednak umnošku iznosa |a| i |b| dvaju vektora a i b i sinusa kuta φ između njih, dakle: |a × b| = |a| |b| sin φ, a smjer okomit na smjerove obaju vektora; preslikavanje koje zadovoljava sljedeća svojstva:

1. a × b = 0 ako je a = 0 ili b = 0 ili ako su vektori a i b kolinearni

2. a × b = −b × a (antikomutativnost)

3. a × (b + c) = a × b + a × c (distributivnost)

4. λ (a × b) = (λa) × b = a × (λb) (homogenost).

Vektorski umnošci jediničnih vektora i, j, k (u pravokutnome Kartezijevu koordinatnom sustavu vektori u smjerovima osi x, y i z) imaju sljedeća svojstva:

1. i × i = j × j = k × k = 0

2. i × j = k, j × k = i, k × i = j

3. j × i = –k, k × j = –i, i × k = –j.

Vektorski umnožak radijvektora a = a_xi + a_yj + a_zk i radijvektora b = b_xi + b_yj + b_zk jest:

a × b = (a_yb_z – a_zb_y) i + (a_zb_x – a_xb_z) j + (a_xb_y – a_yb_x) k ili

.

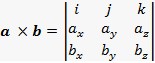Za dvostruki vektorski umnožak vrijedi: (a × b) × c = (a · c) b – (b · c) a.