skalarni umnožak (skalarni produkt), skalar jednak umnošku iznosa |a| i |b| dvaju vektora a i b i kosinusa kuta φ koji vektori zatvaraju, dakle: a · b = |a| |b| cos φ; preslikavanje koje na vektorskom prostoru X nad poljem K realnih ili kompleksnih brojeva svakomu paru vektora a, b iz vektorskoga prostora X pridružuje broj iz polja brojeva K i zadovoljava sljedeća svojstva:
1. a · b = 0 ako je a = 0 ili b = 0 ili a ⊥ b
2. a · b > 0 ako je kut između vektora a i b manji od π/2
3. a · b < 0 ako je kut između vektora a i b veći od π/2
4. a · b = b · a (komutativnost)
5. a · (b + c) = a · b + a · c (distributivnost)
6. λ (a · b) = (λ a) · b = a · (λ b) (homogenost), gdje je λ broj.
Skalarni umnošci jediničnih vektora i, j, k (u pravokutnome Kartezijevu koordinatnom sustavu vektori u smjerovima osi x, y i z) imaju sljedeća svojstva:
1. i · i = j · j = k · k = 1
2. i · j = j · i = j · k = k · j = k · i = i · k = 0.
Skalarni umnožak radijvektora a = axi + ayj + azk i radijvektora b = bxi + byj + bzk jest:
a · b = axbx + ayby + azbz.
Ako je na vektorskom prostoru X zadan skalarni produkt, vektorski prostor X se naziva unitarnim prostorom. Osnovni primjer trodimenzionalan je prostor s ishodištem O i sa skalarnim umnoškom
(OT | OT') = OT · OT' · cosφ,
gdje je φ kut koji zatvaraju radijvektori OT i OT'. Broj √ (x | x) označuje se sa | x | i naziva norma ili duljina vektora x. Norma zadovoljava tzv. nejednakost trokuta: |x + y| ≤ | x | + | y |. Vektor x je ortonormiran ako je | x | = 1. Baza vektorskoga prostora X je ortonormirana ako su joj svi članovi normirani i međusobno ortogonalni. Ako je (ei) takva baza, za svaki vektor x vrijedi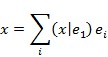 
. Osim konačnodimenzionalnih, osobito važni unitarni prostori jesu Hilbertovi prostori, koji su unijeli geometrijski zor u probleme funkcionalne analize.
