metoda najmanjih kvadrata, metoda za obradbu eksperimentalnih podataka s elementima numeričke matematike i statistike koja omogućava dobivanje funkcionalne ovisnosti mjerenih veličina iz eksperimentalnih podataka. Funkcija i vrijednosti parametara funkcije određuju se tako da je zbroj kvadrata razlika između izmjerenih i izračunanih vrijednosti minimalan, odnosno, određuje se funkcija kojoj krivulja prilazi što bliže danim točkama. Dobivena funkcionalna ovisnost omogućava predviđanje vrijednosti mjerene veličine u područjima koja nisu obuhvaćena mjerenjem. Metodu su neovisno jedan o drugome otkrili Adrien-Marie Legendre i Carl Friedrich Gauss.
Primjerice, ako se rezultati n mjerenja prikažu u dvodimenzijskome pravokutnom Kartezijevu koordinatnom sustavu gdje i-tom rezultatu mjerenja odgovaraju koordinate i-te točke (xi i yi), jednadžba linearne funkcije: y = ax + b, koja najbolje odgovara rezultatima mjerenja, može se naći s pomoću izraza:
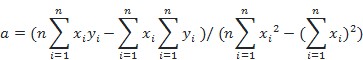 ,
,
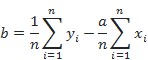 .
.