gama-funkcija (znak Γ), jedinstvena kompleksna funkcija definirana u cijeloj kompleksnoj ravnini osim u negativnim cijelim brojevima i nuli, a u pozitivnim cijelim brojevima podudara se s Γ (n) = (n − 1)!, gdje je n pozitivni cijeli Primjerice, Γ (1) = (1 − 1) = 0! = 1, Γ (2) = (2 − 1)! = 1! = 1, Γ (3) = (3 − 1)! = 2! = 2, Γ (4) = (4 − 1)! = 3! = 6. Leonhard Euler definirao je gama-funkcije kako bi faktorijel mogao proširiti i na sve realne pozitivne brojeve.
Za kompleksni broj z, kojemu je realni dio veći od nule, Re z > 0, gama-funkcija definirana je integralom:
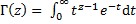 .
.
(→ eulerovi integrali)
Osnovna svojstva gama-funkcija:
Γ (n) = (n − 1)!
Γ (1/2) = √ π
Γ (–1/2) = –2√ π
Γ (3/2) = (1/2)√ π
Γ (–3/2) = (4/3)√ π
Γ (x + 1) = xΓ (x)
Γ (x) Γ (1 – x) = π/sin πx.