metoda brojenja kutija, način određivanja necjelobrojnih dimenzija fraktala. Tako određena fraktalna dimenzija naziva se i dimenzija brojenja kutija (engl. box-counting dimension). Osnovna je ideja metode da se npr. duljina krivulje, površina plohe i volumen tijela (kocke npr.) izmjere tako da se elementi najveće dimenzije (u ovom slučaju trodimenzijske elementarne kocke) poslažu kao kutije duž krivulje, na plohu ili u volumen tijela, te da ih se prebroji. Općenito vrijedi da će broj elemenata kojim će se prekriti skup S biti obrnuto razmjeran veličini »kutije«:
N(S) ~ 1/εd,
gdje je N(S) broj elemenata, ε linearna dimenzija »kutije«, a d općenito pretpostavljena fraktalna dimenzija. Nuždan je i dovoljan uvjet za to da postoji pozitivna konstanta k tako da vrijedi:
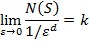
Ako se ta relacija logaritmira i sredi, slijedi za fraktalnu dimenziju d:
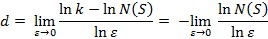
Važno je uočiti da »kutija« može biti bilo kojeg oblika i bilo koje dimenzije d, ne samo cjelobrojne, što ovisi o svojstvima skupa S koji se premjerava. U nekim slučajevima tako izračunana fraktalna dimenzija može biti jednaka topološkoj, kao što je to npr. za skup točaka A određenih geometrijskim nizom:
A ( 0, 1/2 , 1/4 , 1/8 , 1/16 , … ).
Općenito, fraktalna je dimenzija širi pojam od topološke dimenzije, koja je uvijek cjelobrojna (općenito n-dimenzionalni skupovi ili geometrijski likovi).