transformacija pravokutnih koordinata, paralelni pomak osi sustava ili vrtnja osi, pri čem stare koordinate (x, y, z) prelaze u nove (x1, y1, z1). Ako je riječ i o pomaku i o vrtnji, transformacije se, zbog međusobne neovisnosti, izvode sukcesivno. Za paralelni pomak vrijede jednadžbe:
| x = x1 + a |
y = y1 + b |
z = z1 + c |
| x1 = x – a |
y1 = y – b |
z1 = z – c, |
gdje su a, b, c koordinate novog ishodišta sustava u starim koordinatama. Za vrtnju vrijede jednadžbe:
| x = l1x1 + l2 y1 + l3z1 |
x1 = l1x + m1y + n1z |
| y = m1x1 + m2 y1 + m3z1 |
y1 = l2x + m2y + n2z |
| z = n1x1 + n2 y1 + n3z1 |
z1 = l3x + m3y + n3z, |
gdje su l1, l2, l3 kosinusi kutova novih osi x1, y1, z1 u odnosu na os x, m1m2m3 u odnosu na os y, a n1n2n3 u odnosu na os z. Kosinusi kutova tvore determinantu transformacije:
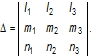
Ako su svi elementi determinante različiti od nule (vrtnja oko sve tri osi), onda se kut v između osi z i z1 naziva kutom nutacije. (→ eulerovi kutovi)