Legendreova diferencijalna jednadžba [ləžᾶ:'dʀ~], linearna diferencijalna jednadžba drugoga reda u obliku:
(1 – x²)y″ – 2xy′ + n(n + 1)y = 0
Za cjelobrojni n rješenja su Legendreovi polinomi (kugline funkcije):
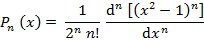
Prva dva polinoma, P0(x) = 1 i P1(x) = x, dovoljna su za izračunavanje sljedećih, jer vrijedi relacija:
(n + 1)Pn+1 (x) = (2n + 1)x P(x) – nPn–1(x)
tako da npr. za n = 1 slijedi:
2P2(x) = (2 + 1)x P1(x) – 1 P0(x)
i uvrštenjem P1(x) = x, P0(x) = 1, slijedi P2(x) = (3x² – 1)/2 itd.