svojstveni polinom (karakteristični polinom) kvadratne matrice A n-toga reda je polinom PA (λ) n-toga stupnja u varijabli λ, koji je zadan kao PA (λ) = det (λI – A), gdje je I jedinična matrica n-toga reda:
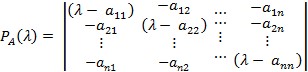
Jednadžba PA(λ) = 0 naziva se svojstvena. Ako je A simetrična i realna, ta se jednadžba naziva i sekularna: u tom su slučaju korijeni te jednadžbe realni. Naziv sekularna potječe od P. S. Laplacea, koji je do takvih jednadžbi došao proučavanjem sekularnih perturbacija u gibanjima planeta (malih odstupanja do kojih dolazi u dugom vremenskom periodu; lat. saeculum: stoljeće).
Ako je A linearni operator na konačno dimenzionalnom vektorskom prostoru, svojstveni polinom PA(λ) od A definira se kao svojstveni polinom matrice koja je tom operatoru pridružena u nekoj bazi prostora. Korijeni svojstvene jednadžbe PA(λ) = 0 upravo su svojstvene vrijednosti operatora A. (→ svojstveni vektor)