kompleksni brojevi, brojevi u obliku uređenih parova oblika a + ib (ili a + bi), gdje su a i b realni brojevi a i je imaginarna jedinica, kojoj je osnovno svojstvo i² = –1. Uvedeni su kako bi kvadratna jednadžba ax² + bx + c = 0 imala rješenje za bilo koji izbor koeficijenata a, b, c. Davno se uočilo da neke kvadratne jednadžbe imaju rješenja u području realnih brojeva, a za neke (kao npr. za x² + 1 = 0) ne postoji nijedno rješenje. Za kompleksni broj z = a + ib, a se naziva realni, a b imaginarni dio od z; oznake su a = Re z, b = Im z. Dva su kompleksna broja z1 = a + ib i z2 = c + id po definiciji jednaka (z1 = z2) ako i samo ako su im jednaki realni i imaginarni dijelovi, tj. a = c i b = d.
Osnovne operacije
Osnovne operacije s kompleksnim brojevima jesu zbrajanje i oduzimanje, množenje i dijeljenje:
1. z1 ± z2 = (a + ib) ± (c + id) = (a ± c) + i (b ± d)
2. z1 · z2 = (a + ib) · (c + id) = (ac – bd) + i (ad + bc)
3. z1 / z2 = (a + ib) / (c + id) = [(ac + bd) + i (bc + ad)] / (c² + d²), ako je c² + d² ≠ 0.
Svojstva zbrajanja i množenja kompleksnih brojeva:
1. z1 · z2 = z2 · z1 ili z1 + z2 = z2 + z1 (komutativnost)
2. (z1 · z2) · z3 = z1 · (z2 · z3) ili (z1 + z2) + z3 = z1 + (z2 + z3) (asocijativnost)
3. (z1 + z2) · z3 = z1 · z3 + z2 · z3 (distributivnost).
Uz tako definirane operacije skup komopleksnih brojeva C je polje. Identificira li se realan broj a s kompleksnim brojem kojemu je imaginarni dio jednak nuli z = a + i0, polje R realnih brojeva postaje smješteno u polju kompleksnih brojeva i to je smještanje u skladu s operacijama. Imaginarni brojevi su kompleksni brojevi koji nemaju realni dio z = 0 + ib, pišu se kraće sa z = ib. Gaussova ravnina obično predočuje polje kompleksnih brojeva tako da je kompleksnomu broju z = a + ib pridružena točka ravnine s apscisom a i ordinatom b. Modul ili apsolutna vrijednost |z| kompleksnog broja z jednaka je udaljenosti točke (a, b) od ishodišta: |z| = √ a² + b² .
Kompleksno konjugirani brojevi su parovi brojeva koji imaju jednake realne, a suprotne imaginarne dijelove. Kompleksni broj z = a + ib kompleksno je konjugiran broju z = a – ib. Umnožak dvaju konjugirano kompleksnih brojeva realan je i nenegativan broj: (a + ib) (a – ib) = a² + b².
Trigonometrijski prikaz kompleksnog broja
Ako su r, φ polarne koordinate točke koja predstavlja kompleksan broj z u ravnini, onda je z = r (cos φ + i sin φ) trigonometrijski prikaz kompleksnog broja, koji je prikladan za potenciranje i korjenovanje (Moivreove formule):
zn = rn [cos (n φ) + i sin (n φ)],
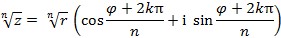 ,
,
gdje je k = 0, 1, …, (n – 1).
U polju kompleksnih brojeva rješive su sve kvadratne jednadžbe s realnim koeficijentima, te jednadžbe proizvoljnog stupnja, kako s realnim tako i s kompleksnim koeficijentima. (→ fundamentalni teorem algebre)
Razvoj kompleksnih brojeva
Pojava imaginarnih i kompleksnih brojeva vrlo je staroga datuma. Tako je već Heron iz Aleksandrije dobio rješenje za √ − 63 , a Geronimo Cardano je 1545. pisao 40 = (5 + √ −15 ) · (5 − √ −15 ). Prvotno se s kompleksnim brojevima računalo samo formalno po analogiji s realnima, odakle je i došlo do naziva imaginarni (zamišljeni, nestvarni). Naziv je zadržan, iako je postao bespredmetnim već uvođenjem Gaussove ravnine i Hamiltonovom definicijom kompleksnih brojeva kao uređenih parova realnih brojeva.
Teorija funkcija kompleksnih varijabli, tj. funkcija definiranih na dijelu kompleksne ravnine i s kompleksnim vrijednostima, isprepleće se s gotovo svim granama moderne matematike, a primjenjuje se u fizici i elektrotehnici.